11.SINIF DİZİLER,ARİTMETİK DİZİLER,GEOMETRİK DİZİLER KONU ANLATIMI
A. TANIM

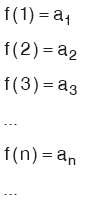











DİZİLER
Tanım kümesi pozitif tam sayılar kümesi olan her
fonksiyona dizi adı verilir.

fonksiyonununda,
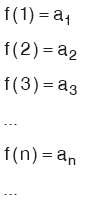
olduğuna göre,
biçiminde yazılabilir.
f fonksiyonu (dizisi) genel olarak,

biçiminde veya kısaca (an)
biçiminde gösterilir.
a1, dizinin 1. terimi (ilk terimi);
a2, dizinin 2. terimi;
a3, dizinin 3. terimi;
...
an, dizinin n. terimi (genel terimi) dir.
Uyarı
1. Genel terimi belirtilmeyen sayı
grupları dizi meydana getirmezler.
2. Diziler değer kümesine göre adlandırılır.
Değer kümesi; reel sayılar kümesi olan dizi reel sayı dizisi, karmaşık
sayılar olan dizi karmaşık sayı dizisi adını alır.
|
B. SONLU DİZİ

Tanım kümesi Ak olan dizilere sonlu
dizi denir.
C. SABİT DİZİ
Bütün terimleri birbirine eşit olan diziye sabit dizi denir.
D. EŞİT DİZİ
Her n pozitif tam sayısı için,
an = bn
ise, (an) ve (bn)
dizilerine eşit diziler denir.
E. DİZİLERLE YAPILAN İŞLEMLER
(an) ve (bn) birer dizi, c bir
reel sayı olmak üzere,

F. MONOTON DİZİLER
Genel terimi an olan bir dizide eğer
her  için,
için,
 için,
için,
Uyarı
 dizisinin monotonluk durumu
aşağıdaki şekilde incelenir: dizisinin monotonluk durumu
aşağıdaki şekilde incelenir:
1. Paydanın kökü (cn + d = 0
denkleminin kökü) 1 den
küçük ise dizi monotondur.
Bu
durumda,
a) ad – bc > 0 ise dizi monoton artandır.
b) ad – bc < 0 ise dizi monoton azalandır.
c) ad – bc = 0 ise dizi sabittir.
2. Paydanın kökü (cn + d = 0
denkleminin kökü) 1 den
büyük ise
dizimonoton
değildir.
|
G. ALT DİZİ
Bir (an) dizisi verilmiş olsun.
(kn) artan bir pozitif tam sayı dizisi
olmak üzere,  dizisine (an)
dizisinin alt dizisi denir ve
dizisine (an)
dizisinin alt dizisi denir ve  biçiminde gösterilir.
biçiminde gösterilir.
 dizisine (an)
dizisinin alt dizisi denir ve
dizisine (an)
dizisinin alt dizisi denir ve  biçiminde gösterilir.
biçiminde gösterilir.
H. DİZİLERİN YAKINSAKLIĞI VE IRAKSAKLIĞI
1. Komşuluk
a ve e birer
reel sayı ve e >
0 olmak üzere,

açık aralığına a nın e (epsilon) komşuluğu denir.
Bu aralığı (kümeyi) T ile gösterirsek,

olur.
T kümesi sayı doğrusunda aşağıdaki gibi
gösterilebilir.
Uyarı
1. (an) dizisinin, a
nın e komşuluğundaki terimleri,
font
color="black">
 |
eşitsizliğini sağlar.
2. (an)
dizisinin, a nın e komşuluğu
dışındaki terimleri,

eşitsizliğini sağlar.
I. YAKINSAK DİZİLER ve IRAKSAK DİZİLER
(an) bir reel sayı dizisi, a sabit bir reel
sayı olsun.
Her e pozitif
reel sayısı için, (an) dizisinin hemen hemen her terimi, a nın e komşuluğunda bulunuyorsa, (an)
dizisi a ya yakınsıyor denir.
(an) dizisi a sayısına yakınsıyorsa; (an)
dizisine yakınsak dizi denir.
Yakınsak olmayan dizilere ıraksak diziler denir.
J. DİZİLERİN LİMİTİ
1. Limitin Tanımı
(an) bir reel sayı dizisi olsun.
(an) dizisi sabit bir a reel sayısına
yakınsıyor ise, a sayısına (an) dizisinin limiti denir.
lim(an) = a
ya da (an) ® a
biçiminde gösterilir.
Kural
1. (an) dizisi bir a reel
sayısına yakınsıyorsa, bu dizinin her alt dizisi de a reel sayısına yakınsar.
Bunun karşıtı doğru değildir.
2. Bir dizinin limiti varsa bir
tanedir.
3.
 olmak üzere, (an)
= (c) ise, olmak üzere, (an)
= (c) ise,
lim(an) = lim(c) = c dir.
(Her sabit dizi yakınsaktır.)
|
2. Limitle İlgili Özellikler
Kural
(an)
ve (bn) birer dizi; a, b, c birer reel sayı olmak üzere,
 |
K. GENİŞLETİLMİŞ REEL SAYILAR KÜMESİ
Reel sayılar kümesine, artı sonsuz (+¥) ve eksi sonsuz (–¥) kavramlarının katılmasıyla elde
edilen
[–¥, +¥]
aralığına (kümesine) genişletilmiş reel sayılar kümesi
denir.
1. Iraksak Diziler
Kural
1. Her K reel sayısı için, (an)
dizisinin hemen hemen her terimi (+¥) un K
komşuluğunda ise (an) dizisinin limiti (+¥) dur veya (an) dizisi (+¥) a ıraksar denir.
2. Her K reel sayısı için, (an)
dizisinin hemen hemen her terimi (–¥) un K komşuluğunda
ise (an) dizisinin limiti (–¥) dur veya (an) dizisi (–¥) a ıraksar denir.
3. (+¥) a veya (–¥) a ıraksayan dizilere ıraksak diziler
denir.
|
2. Genişletilmiş Reel Sayılar Kümesinde İşlemler


Kural
Dizilerin
limitleri bulunurken elde edilen,

ifadeleri
belirsizdir.
|
Kural
 |
Kural
 |
Kural
(an)
bir dizi; c bir reel sayı olmak üzere,
 |
Kural
(an)
bir dizi olmak üzere,
 |
Uyarı
(1n)
sabit dizisi ile
 dizisi birbirine
karıştırılmamalıdır. dizisi birbirine
karıştırılmamalıdır. |
Uyarı
Genel
terimi rasyonel kesir olan dizilerin limitinin hesaplanmasında, aşağıdaki
sıralama kullanılır.
 |
Kural
 |
Kural
(an)
pozitif terimli bir dizi olsun.
 |
3. Belirsizlik Durumları
a.  Belirsizliği
Belirsizliği
 Belirsizliği
Belirsizliği
Bu tür belirsizlikleri daha önce verdiğimiz kural
yardımı ile sonuçlandırabiliriz.
b. 0 . ¥
Belirsizliği
Bu tür belirsizlikler,  belirsizliğine dönüştürülerek
limit bulunur.
belirsizliğine dönüştürülerek
limit bulunur.
 belirsizliğine dönüştürülerek
limit bulunur.
belirsizliğine dönüştürülerek
limit bulunur.
c. ¥ – ¥ Belirsizliği

¥ – ¥ tipindeki belirsizlikleri
cebirsel işlemler yaparak giderebiliriz.
Kural

Bu
belirsizliği ortadan kaldırmak için, (an) dizisinin payı ve
paydası
 ifadesiyle genişletilir. ifadesiyle genişletilir. |
Uyarı
 dizisinde
(+¥) – (+¥) belirsizliği vardır. dizisinde
(+¥) – (+¥) belirsizliği vardır. dizisinde
belirsizlik söz konusu dizisinde
belirsizlik söz konusu
değildir.
Bu dizide (+¥) + (+¥) durumu vardır.
(+¥) + (+¥) = +¥
olduğu
için, bu dizi +¥ a ıraksar.
|
Kural
a >
0 olmak üzere,

olur.
|
L. SINIRLI DİZİLER
1. Üst Sınır
Her  için, an £ M olacak şekilde bir M reel
sayısı varsa (an) dizisine üstten sınırlıdır denir.
için, an £ M olacak şekilde bir M reel
sayısı varsa (an) dizisine üstten sınırlıdır denir.
 için, an £ M olacak şekilde bir M reel
sayısı varsa (an) dizisine üstten sınırlıdır denir.
için, an £ M olacak şekilde bir M reel
sayısı varsa (an) dizisine üstten sınırlıdır denir.
M sayısı da bu dizinin üst sınırı adını alır. M den
büyük her reel sayı da (an) dizisinin üst sınırıdır.
Üstten sınırlı bir dizinin üst sınırlarından en küçük
olanına dizinin en küçük üst sınırı (Eküs) denir.
(an) dizisinin Eküs ü, Eküs(an)
biçiminde gösterilir.
2. Alt Sınır
Her  için, m £ an olacak
şekilde bir m reel sayısı varsa (an) dizisine alttan sınırlıdır
denir.
için, m £ an olacak
şekilde bir m reel sayısı varsa (an) dizisine alttan sınırlıdır
denir.
 için, m £ an olacak
şekilde bir m reel sayısı varsa (an) dizisine alttan sınırlıdır
denir.
için, m £ an olacak
şekilde bir m reel sayısı varsa (an) dizisine alttan sınırlıdır
denir.
m sayısı da bu dizinin alt sınırı adını alır. m den
küçük her reel sayı da (an) dizisinin alt sınırıdır.
Alttan sınırlı bir dizinin alt sınırlarından en büyük
olanına dizinin en büyük alt sınırı (Ebas) denir.
(an) dizisinin Ebas ı, Ebas(an)
biçiminde gösterilir.
3. Sınırlı Diziler
Hem alttan hem de üstten sınırlı olan dizilere,
sınırlı diziler denir.
Uyarı
1. Sınırlı bir dizide Eküs ve Ebas
dizinin elemanı olmayabilir.
2. Monoton bir dizinin yakınsak olması
için gerek ve yeter koşul, sınırlı olmasıdır.
3. Yakınsak her dizi sınırlıdır. Bu
ifadenin karşıtı doğru olmayabilir.
4. Monoton ve yakınsak bir dizinin,
ilk terimi ile limitinden; büyük olanı Eküs, küçük olanı Ebas tır.
|
